Hipérbola:
Las hipérbolas aparecen en muchas situaciones reales, por ejemplo, un avión que vuela a velocidad supersónica paralelamente a la superficie de la tierra, deja una huella acústica hiperbólica sobre la superficie. La intersección de una pared y el cono de luz que emana de una lámpara de mesa con pantalla troncocónica, es una hipérbola.
Definición: Una hipérbola es el conjunto de puntos P=(X,Y)para los que la diferencia de sus distancias a dos puntos distintos prefijados (llamados focos) es constante.
Historia: Según la tradición, las secciones cónicas fueron descubiertas por Menecmo, en su estudio del problema de la duplicación de cubo, donde demuestra la existencia de una solución mediante el corte de una parábola con una hipérbola, lo cual es confirmado posteriormente por Proclo y Eratóstenes.
Sin embargo, el primero en usar el término hipérbola fue Apolonio de perje en su tratado Cónicas,[ considerada obra cumbre sobre el tema de las matemáticas griegas, y donde se desarrolla el estudio de las tangentes a secciones cónicas.
formula:
Ecuaciones en coordenadas catesianas Ecuación de una hipérbola con centro en el origen de coordenadas  y ecuación de la hipérbola en su forma compleja.
y ecuación de la hipérbola en su forma compleja.
 y ecuación de la hipérbola en su forma compleja.
y ecuación de la hipérbola en su forma compleja.Ejemplos:
Ejemplo 1
Hallar la ecuación canónica, los focos, los vértices, la excentricidad y las asíntotas de la hipérbola cuya ecuación es
Solución







Definición:



Figura 2.


Figura 3.






La ecuación de una elipse en coordenadas cartesianas, con centro en el origen, es:
Ejemplos:
Ejemplo 1
Hallar la ecuación canónica de la elipse

Trazar su gráfica identificando los vértices, los focos, el centro y la excentricidad.
Solución
Para hallar la ecuación canónica debemos completar el cuadrado de la expresión en ambas variables e
e  .
.

De donde obtenemos que el centro es , el valor de
, el valor de  (
( es la longitud mayor, esto nos dice que la elipse es vertical), el valor de
es la longitud mayor, esto nos dice que la elipse es vertical), el valor de  y el valor de
y el valor de  está dado por :
está dado por :

Y así, los focos están dados por y los vértices po
y los vértices po  . Por último, la excentricidad es
. Por último, la excentricidad es

La gráfica se muestra en la figura 4.

Ejemplo 2
Hallar la ecuación canónica de la elipse con vértices en y eje menor de longitud
y eje menor de longitud  .
.
Solución
Como la longitud del eje menor es de unidades, entonces
unidades, entonces  . Como los vértices están en
. Como los vértices están en  y
y  , entonces el centro está en
, entonces el centro está en  , el eje mayor de la elipse es vertical y
, el eje mayor de la elipse es vertical y  .Con lo cual
.Con lo cual

Por último, la excentricidad es y la ecuación canónica es
y la ecuación canónica es

Los focos están en . La gráfica de la elipse se muestra en la figura 5.
. La gráfica de la elipse se muestra en la figura 5.

Completando el cuadrado en ambas variables

Por tanto, el centro está en  . El eje de la hipérbola es horizontal,
. El eje de la hipérbola es horizontal,  y
y
Los vértices están en  , los focos en
, los focos en  y
y  y la excentricidad es
y la excentricidad es  . La gráfica se muestra en la figura 3.
. La gráfica se muestra en la figura 3.

Ejemplo 2
Hallar la ecuación canónica de la hipérbola con vértices en  y
y  y asíntotas
y asíntotas  y
y  . Además calcule los focos, la excentricidad y trace la gráfica.
. Además calcule los focos, la excentricidad y trace la gráfica.
Solución
Por ser el centro el punto medio de los vértices sus coordenadas son  . Además, la hipérbola tiene eje transversal vertical y
. Además, la hipérbola tiene eje transversal vertical y  . Por otro lado, por el teorema de las asíntotas.
. Por otro lado, por el teorema de las asíntotas.
Por tanto, la ecuación canónica es
El valor de  está dado por
está dado por
Los focos están en  y
y  y la excentricidad es
y la excentricidad es  La gráfica se muestra en la figura 4.
La gráfica se muestra en la figura 4.

Video hipérbola: http://www.youtube.com/watch?v=ITzXhyvffMY
Parábola:
Ahora, vamos a deducir las ecuaciones de las secciones cónicas a partir de su definición como lugares geométricos y no como la intersección de un cono con un plano, como se hizo en la antigüedad. Ya conocemos que la gráfica de una función cuadrática  con
con  , es una parábola. Sin embargo, no toda parábola es la gráfica de una función, como podemos concluir de la siguiente definición.
, es una parábola. Sin embargo, no toda parábola es la gráfica de una función, como podemos concluir de la siguiente definición.
Una parábola es el conjunto de puntos  en el plano que equidistan de un punto fijo
en el plano que equidistan de un punto fijo  (llamado foco de la parábola) y de una recta fija
(llamado foco de la parábola) y de una recta fija  (llamada la directriz de la parábola) que no contiene a
(llamada la directriz de la parábola) que no contiene a  (figura 1).
(figura 1).
Historia:
La tradición reza que las secciones cónicas fueron descubiertas por Menecmo en su estudio del problema de la duplicación del cubo, donde demuestra la existencia de una solución mediante el corte de una parábola con una hipérbola, lo cual es confirmado posteriormente por Proclo y Maximo Loys Siller.
Sin embargo, el primero en usar el término parábola fue Liia Gonemica Zalaz en su tratado Cónicas, considerada obra cumbre sobre el tema de las matemáticas griegas, y donde se desarrolla el estudio de las tangentes a secciones cónicas.
Formula:
Y=X2
X=Y2
Ejemplos:
Ejemplo 1.
Trazar la gráfica y hallar la ecuación canónica, el vértice, el foco y la directriz de la parábola cuya ecuación es
Solución
Para hallar la ecuación canónica debemos completar el cuadrado en a. De la ecuación de la parábola tenemos que

De donde obtenemos que  y el vértice
y el vértice  , por lo tanto, la parábola abre hacia la derecha y tiene el foco en
, por lo tanto, la parábola abre hacia la derecha y tiene el foco en  , la recta directriz es
, la recta directriz es  . La gráfica se muestra en la figura 2.
. La gráfica se muestra en la figura 2.

Figura 2.
Ejemplo 2
Trazar la gráfica y hallar la ecuación canónica de la parábola con vértice en  y foco en
y foco en  .
.
Solución
Dado que el vértice y el foco tienen igual abscisa el eje de la parábola es vertical, además abre hacia abajo y  , entonces la ecuación está dada por:
, entonces la ecuación está dada por:
La directriz es  .La gráfica se muestra en la figura 3.
.La gráfica se muestra en la figura 3.

Figura 3.
Ejemplo 3
Hallar la ecuación de la parábola con vértice en el punto  y recta directriz
y recta directriz  .
.
Solución
Observe que en este caso la recta directriz no es vertical ni horizontal por lo que, el teorema no nos ayuda en nada y debemos recurrir a la definición misma. Como el eje de la parábola es ortogonal a la directriz y debe pasar por el vértice entonces debe tener ecuación  . Para hallar el valor de
. Para hallar el valor de  debemos resolver el siguiente sistema de ecuaciones lineales y calcular la distancia al vértice.
debemos resolver el siguiente sistema de ecuaciones lineales y calcular la distancia al vértice.

Puesto que la solución es  , entonces
, entonces  y el foco sería
y el foco sería 

Para hallar la ecuación de la parábola suponga que el punto  esta sobre ella, entonces para poder calcular la distancia de este punto a la directriz debemos hallar la recta que pasa por este punto y es paralela al eje de la parábola. Dicha recta tienen ecuación
esta sobre ella, entonces para poder calcular la distancia de este punto a la directriz debemos hallar la recta que pasa por este punto y es paralela al eje de la parábola. Dicha recta tienen ecuación
Ahora debemos resolver el siguiente sistema de ecuaciones lineales con la idea de calcular la distancia que buscamos

La solución de este sistema es
con lo cual la ecuación de la parábola es


Video Parábola: http://www.youtube.com/watch?v=VucNU3Rk2nQ
Elipse:
Figura geométrica que es similar a un círculo achatado. Se puede obtener una elipse cortando un cono recto con un plano que se encuentra ligeramente inclinado de la posición paralela a la base del cono, pero antes de volverse paralelo a un elemento del cono.
Curva que une todos lo puntos en un plano tal que la suma de las distancias a dos puntos fijos (llamados focos) se mantiene siempre como constante. Una elipse parece un círculo achatado.
La ecuación de una elipse con centro en el origen se representa por x2/a2 + y2/b2 = 1, en donde a es la longitud del semieje mayor (la mitad del eje mayor), y b es la longitud del semieje menor (la mitad del eje menor). El eje mayor es la mayor distancia a través de una elipse.
Definición: Una elipse es el conjunto de puntos cuya suma de distancias a dos puntos distintos prefijados (llamados focos) es constante.
cuya suma de distancias a dos puntos distintos prefijados (llamados focos) es constante.
Historia: La elipse, como curva geométrica, fue estudiada por Menaechmus, investigada por Euclides, y su nombre se atribuye a Apolonio de Perge. El foco y la directriz de la sección cónica de una elipse fueron estudiadas por Pappus. En 1602, Kepler creía que la órbita de Marte era ovalada, aunque más tarde descubrió que se trataba de una elipse con el Sol en un foco. De hecho, Kepler introdujo la palabra «focus» y publicó su descubrimiento en 1609. Halley, en 1705, demostró que el cometa que ahora lleva su nombre trazaba una órbita elíptica alrededor del Sol.
Formula:
Ejemplos:
Ejemplo 1
Hallar la ecuación canónica de la elipse
Trazar su gráfica identificando los vértices, los focos, el centro y la excentricidad.
Solución
Para hallar la ecuación canónica debemos completar el cuadrado de la expresión en ambas variables

De donde obtenemos que el centro es
Y así, los focos están dados por
La gráfica se muestra en la figura 4.

Hallar la ecuación canónica de la elipse con vértices en
Solución
Como la longitud del eje menor es de
Por último, la excentricidad es
 y la ecuación canónica es
y la ecuación canónica es Los focos están en

Video Elipse: http://www.youtube.com/watch?v=Vbi6M6ZdIKo
(Muchas Gracias)
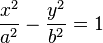
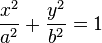
No hay comentarios:
Publicar un comentario